20. Diffraction par des structures périodiques.

PPT

Diffraction par des structures periodiques (2.08 Mo)

PDF

Diffraction par des structures periodiques (1.64 Mo)

Prérequis

• Interférence par les fentes d'Young
• Diffraction de Fraunhofer (cours précédent)
• Cristallographie

Introduction

Au cours précédent, on a étudié la diffraction de Fraunhofer par une fente simple.

Dans ce cours, on se demande ce qu'il se passe si on multiplie le nombre de fentes?

On va voir dans cette leçon que la multiplication du nombre de fentes à un intérêt, d'abord en optique, puis on généralisera ce principe à d'autres domaines de la physique.

I. Le réseau plan en optique

1) Présentation d'un réseau de diffraction

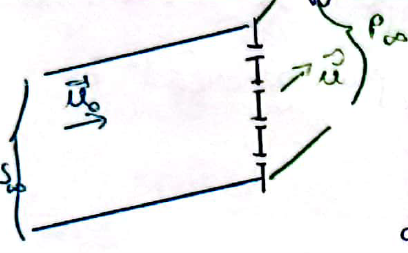
• Réseau de diffraction: Toute structure périodique qui peut diffracter une onde lumineuse ou électromagnétique. sur slide
• Réseau 1D: Structure plane dont le coefficien de réflexion ou de transmission est périodique dans une direction.  sur slide

• Fabrication: Réseau de fentes ou réseau gravé dans une plaque de verre

2) Ordre d'interférence et éclairement

• Un réseau est composé de traits de grandes longueur, donc la diffraction a lieu uniquement suivant la largeur.
• Position des maximums d'intensité:   image de la figure de diffraction sur python

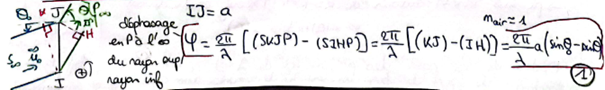
Maximum d'intensité ⇔ Interférences constructives entre toutes les ondes diffractées
                                 ⇔ Les ondes diffractées sont en phase en P
                                 ⇔ φ = -k2π avec k dans Z  
                                 ⇔ 2πa/λ (sinθ₀ - sinθ) = -k2π
                                 ⇔ sinθ - sinθ₀ = kλ/a     Formule des réseaux en transmission

• Intensité diffractée par un réseau de fentes infiniment fines:

Les différentes ondes diffractées sont issues d'une source ponctuelle monochromatique, donc sont cohérentes, donc:
S(P) = S₁(P) + S₂(P) + ... + S_N(P)     avec   S₂(P) = S₁e^-jφ  ....  S_N(P) = S₁e^-j(N-1)φ

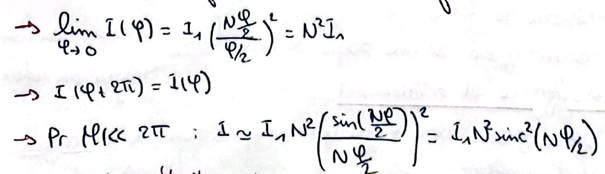
Pic très étroits autour de k = k2π (interférences constructives) ⇔ sinθ₀ + kλ/a = sinθ

• En pratique, les fentes n'ont pas une largeur infiniment fine:

• Dépendance de la position des pics en fonction de λ et de a
• Donc il est possible de faire de la spectroscopie ou de remonter aux caractéristiques de la structure duffractante à partir de l'étude de la figure de diffraction.

3) Application à la spectroscopie

• Spectroscopie: Etudier des spectres émis par une source lumineuse
• Pouvoir de résolution:  sur slide

• Pouvoir dispersif: Un réseau décompose la lumière de la source. Donc un réseau est dispersif.
  • On a:
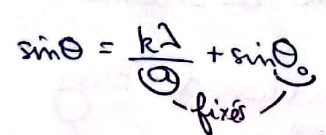
  • Pour k donné, si λ varie de dλ, alors θ varie de dθ avec: cosθ dθ = λdλ/a ⇒
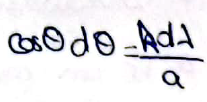
  • En incidence normale pour |k|>0:
  • 

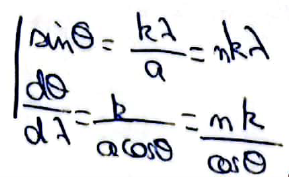
Manip pour remonter aux longeurs d'onde des raies du mercure. Détaillé dans le PDF joint et au niveau du code. sur slide

⇒ On a utilisé les propriétés d'un réseau pour obtenir des informations sur le spectre d'une source. On va maintenant faire l'inverse et remonter au propriétés d'un cristal diffractant.

II. Diffraction des rayons X par des structures périodiques cristallines

Pour cette partie, voir le début du Ashcroft - Physique des solides

1) Position du problème

• Définition d'un cristal et d'un réseau de Bravais sur slide
• Pour obtenir une figure de diffraction d'une onde électromagnétique, il faut: λ ≈ d_atome-atome ≈ qqs Å (1Å = 10^-10m)
• On prend donc: λ ≈ 1Å ≈ 10^-10m
• D'où: ν = c/λ = 10⁸/10^-10 = 10¹⁸ Hz
• Donc on utilise des rayons X pour étudier les structures cristallines

2) Formulation de Bragg

• On envoie des rayons X sur un réseau de Bravais.
• Pour certaines longueurs d'ondes et certaines orientation du réseau, on observe des pics intenses de rayonnement diffracté: les pics de Bragg   schéma sur slide

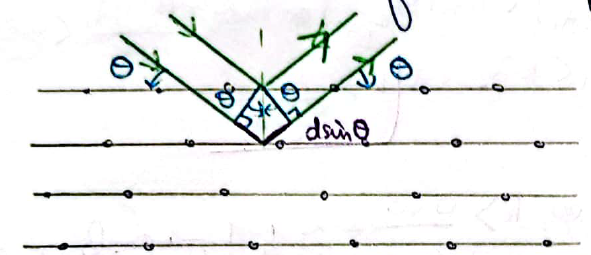
• Inteférences constructives:
  • φ = n2π    avec n dans Z  
  • 2πδ / λ = n2π    avec δ=2d sinθ
  • nλ = 2d sinθ  Condition de Bragg

3) Application à la caractérisation d'une maille cristalline

• Connaissant λ et θ, on peut remonter à d
• Pour un même cristal, plusieurs d sont possibles en fonction de l'orientation du cristal
• On combinant les différents d, on peut remonter à la structure du cristal.

Conclusion

La diffraction peut être un phénomène non désiré car il cause une limite du pouvoir de résolution?

Par contre, la diffraction peut aussi être utile, car à partir d'une figure de diffraction on peut remonter à des informations sur l'objet diffractant ou sur la sources des ondes.

Code

Pour la manip, faire le I.3) et le I.4) de du poly joint.

Agreg interne poly tp extrait optique (1.2 Mo)

import numpy as np
import numpy.random as npr
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.integrate import odeint

# Definition de la fonction affine
def f_aff(x, a, b):
    return a*x+b

# Montecarlo

def montecarlo(X, Y, uX, uY, N_mc=100):
    sigma_X = uX*np.ones(X.size)
    sigma_Y = uY*np.ones(Y.size)

    param = np.zeros((2,N_mc))
    for i in range(N_mc):
        x_mc = npr.normal(loc=X, scale=sigma_X)
        y_mc = npr.normal(loc=Y, scale=sigma_Y)
        pop, pcov = curve_fit(f_aff, x_mc, y_mc)
        param[0,i] = pop[0]
        param[1,i] = pop[1]

    x_th = np.linspace(X.min(), X.max(), 4)
    y_th = f_aff(x_th, *pop)
    for i in range(N_mc):
        y_th = f_aff(x_th, *param[:,i])
        plt.plot(x_th, y_th, 'r', alpha=0.05)
    plt.errorbar(X, Y, xerr=uX, yerr=uY, fmt='+', capsize =3)
    #plt.show()

    a_moy = np.mean(param[0,:])
    a_sig = np.std(param[0,:]) #ecart type
    b_moy = np.mean(param[1,:])
    b_sig = np.std(param[1,:]) #ecart type
    print("La pente moyenne sur les ", N_mc, "mesures est de :", np.round(a_moy,4))
    print("L'écart type entre les pentes des", N_mc, "mesures est de :", np.round(a_sig,4))
    print("Le résultat est donc de :", f"a = {a_moy:.3f} +/- {a_sig:.3f}")
    print("Cela correspond à une erreur de:", f"a_rel = {a_sig/a_moy*100:.0f} %")
    return a_moy, a_sig, b_moy, b_sig

 

In [244]:

n = 1000e3  # nbre de traits du réseau / m
a = 1 / n
L = 2e-5  # longueur du réseau en m  # exagérement petit pour voir le graphique
N = n * L
I0 = 1
theta_0 = 0 * np.pi / 180  # en radians
Lambda = 650e-9
theta = np.linspace(-np.pi/2, np.pi/2, 1000000)
phi = 2 * np.pi / Lambda * a * (np.sin(theta_0) - np.sin(theta))

# Intensité lumineuse réseau
I = I0 * (np.sin(N * phi / 2) / np.sin(phi / 2))**2

# Intensité lumineuse interférence à 2 ondes
I2 = N**2 * I0 / 2 * (1 + np.cos(phi))

# Représentation graphique
plt.figure(figsize=(6, 4))
plt.plot(np.sin(theta), I, label='interférences à N ondes')
#plt.plot(np.sin(theta), I2, label='interférences à 2 ondes')
plt.annotate('', xy=(-0.04, 10), xytext=(0.04, 10), arrowprops=dict(arrowstyle='|-|', color='darkorange', lw=2))
plt.annotate(r'$\frac{\lambda}{L}$', xy=(-0.04, 25), xytext=(0.06, 25), color='darkorange', fontsize=15)
plt.annotate('Ordre -1', xy=(-0.6, 300), xytext=(-0.6, 300), color='black', fontsize=12)
plt.annotate('Ordre 0', xy=(0.05, 300), xytext=(0.05, 300), color='black', fontsize=12)
plt.annotate('Ordre 1', xy=(0.7, 300), xytext=(0.7, 300), color='black', fontsize=12)
plt.xticks([np.sin(theta_0) - Lambda/a, np.sin(theta_0), np.sin(theta_0) + Lambda/a], [r'$sin(\theta_0) - \frac{\lambda}{a}$', r'$sin(\theta_0)$', r'$sin(\theta_0) + \frac{\lambda}{a}$'])
plt.yticks([N**2 * I0], [r'$N^2 I_0$'])
plt.xlabel(r'$sin(\theta)$')
plt.ylabel('Intensité lumineuse')
plt.title('Intensité lumineuse en fonction de l\'angle de sortie')
# plt.legend()
plt.show()

 

 

 

In [261]:

# Données
Lambda = np.array([579.0, 576.9, 546.0, 491.6, 435.8, 407.8, 404.6]) * 10**-9 # en nm - jaune, jaune, vert, vert-bleu (faible), bleu-indigo, violet (faible)
x = np.array([]) * 10**-2  # en m - distance entre la raie considérée et la tache centrale. attention à aller dans l'ordre des longueurs d'ondes définies au dessus
ux = 1e-3  # en m

# Graphique
a_moy, a_sig, b_moy, b_sig = montecarlo(Lambda * 10**9, x*10**2, 0, ux*10**2, N_mc=100)  # a_moy = kD/a
plt.xlabel(r'$\lambda$' + ' (en nm)')
plt.ylabel('x (en cm)')
plt.title('Longueur d\'onde en fonction du déplacement')
plt.show()

# Nombre de traits par unité de longueur du réseau
k = 1
D = 20.5e-2  # en m
uD = 2e-3  # en m
n = a_moy * 10**7 / (k * D)  # 10**7 pour avoir a_moy adimensionnel
un = n * np.sqrt((a_sig*10**7/(a_moy * 10**7))**2 + (uD/D)**2)
print('Le nombre de traits par unité de longueur du réseau est: n = ', np.round(n * 10**-3, 0), '(+/-)', np.round(un * 10**-3, 0), 'traits/mm')
print('Soit: n = ', np.round(n * 10**-3, 0), '(+/-)', np.round(un * 10**-3, 0), 'traits/mm')

 

 

La pente moyenne sur les  100 mesures est de : 0.0117
L'écart type entre les pentes des 100 mesures est de : 0.0005
Le résultat est donc de : a = 0.012 +/- 0.000
Cela correspond à une erreur de: a_rel = 4 %

 

 

Le nombre de traits par unité de longueur du réseau est: n =  569.0 (+/-) 24.0 traits/mm
Soit: n =  569.0 (+/-) 24.0 traits/mm

def find_coord(y, a, b):
    x = (y - b) / a
    return x

 

In [270]:

# Coordonnées du point trouvé
x_r =  # en cm - position de la nouvelle raie par rapport au centre de la figure de diffraction. 
ux_r = 0.1  # en cm
Lambda_r = find_coord(x_r, a_moy, b_moy)
uLambda_r = Lambda_r * np.sqrt((ux_r/x_r)**2 + (a_sig/a_moy)**2)
print('La longueur d\'onde recherchée est: lambda = ' + str(np.round(Lambda_r, 0)) + ' (+/-) ' + str(np.round(uLambda_r)) + ' nm')

# Graphique
plt.figure()
plt.plot(Lambda*10**9, x*10**2, 'o')  # Points de mesure
plt.plot(np.linspace(400, 800), a_moy * np.linspace(400, 800) + b_moy)  # Courbe d'étalonnage
plt.plot(np.linspace(400, Lambda_r), x_r * np.ones(50), linestyle='--', color='grey')  # Ligne horizontale
plt.plot(Lambda_r * np.ones(50), np.linspace(4, x_r), linestyle='--', color='grey')  # Ligne horizontale
plt.xlabel(r'$\lambda$' + ' (en nm)')
plt.ylabel('x (en cm)')
plt.title('Longueur d\'onde en fonction du déplacement')
plt.xlim([400, 700])
plt.ylim([4, 8])
plt.show()

 

 

La longueur d'onde recherchée est: lambda = 661.0 (+/-) 29.0 nm