19. Diffraction de Fraunhofer.

PPT

Diffraction de fraunhofer (6.46 Mo)

PDF

Diffraction de fraunhofer (2.64 Mo)

Diffraction mini montage (1.58 Mo)

Prérequis

• Optique génométrique et ondulatoire
• Interférences
• Transformée de Fourier

Introduction

• Diffraction étudiée pour la 1^ère fois au XVII^ème siècle par l'italien Grimaldi qui proposa le mot "diffraction" qui signifie "briser en morceaux".
• Elle a déjà été vue au lycée et peut facilement être observée par la diffraction d'un rayon laser par une fente fine. Manip introductive avec une fente de + en + fine
• On parle de diffraction optique lorsque les lois de l'optique géométrique ne sont pas respectées.
• La diffraction est un problème important, en particulier dans les montages optique tels que les téléphones ou les microscopes. En effet, elle limite la résolution des instruments d'optique, comme on le verra par la suite avec le critère de Rayleigh.
• Il existe de la diffraction dans tous les phénomènes ondulatoires.

I. La diffraction

1) Principe de Huygens Fresnel (1678 - 1818)

• Modèle ondulatoire de la lumière pour expliquer la diffraction

• Enoncé du principe d'Huygens Fresnel  sur slide
  • Tout élément de surface d∑_M d'une surface atteinte par une onde monochromatique se comporte comme une source secondaire émettant une ondelette sphérique de même fréquence et d'amplitude complexe proportionnelle à d∑_M et à l'amplitude complexe de l'onde incidente en M
  • Les différentes ondelettes sont cohérentes, donc interfèrent entre elles

• D'après H-F:

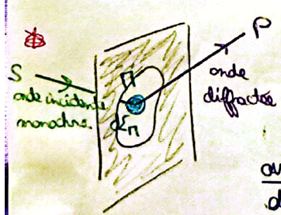
et: MP ≈ cte si P loin de l'écran ⇒ MP >> λ Validité de H-F

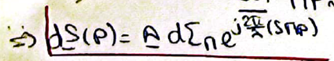
Les différentes ondelettes sont cohérentes entre elles, d'où:

⇒Expression mathématique du ppe d'H-F. Quel est le lien avec la diffraction de Fraunhofer?

2) Diffraction de Fraunhofer

• En diffraction de Fraunhofer, on se place à l'infini (d'où l'approximation de champ lointain ci-dessous):
• On calcule la différence de marche et on pose les vecteurs d'ondes k et k₀. ce qui permet d'exprimer dS en fonction des vecteurs d'onde. Expliciter le sens des termes

• Pour faire les calculs plus facilement, on projette les vecteurs d'onde sur des axes e_x, e_y et e_z: (sur slide)

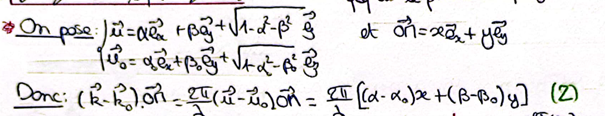
• Avec un écran diffractant quelconque:

Exemples de fonctions de transmission sur slide

• On obtient finalement: (1) + (2) + (3) et parce que les ondelettes sont cohérentes entre elles:

Monter et montrer le montage de la diffraction de Fraunhofer
 

3) Propriétés

Faire manips quali en direct pour illustrer les propriétés, en particulier Babinet

• Translation de la pupille
  • Translation de x₀ suivant e_x (idem selon e_y) : t'(x - y) = t(x-x₀, y)
    • D'où avec: x' = x - x₀
  • Eclairement inchangé par translation de la pupille:
• Dilatation de la pupille
  • Dilatation d'un facteur µ suivant x de la pupille: t'(x, y) = t(x/µ, y)
  • D'où:
• Linéarité - Théorème de Babinet
  • Deux pupille de transparence complexe t₁ et t₂ sont complémentaires si pour tout P de ∑, t₁(P) + t₂(P) = 1 
  • La figure de diffraction produite par deux pupilles complémentaires est la même, sauf dans la direction de l'optique géométrique fente ⇔ trait

⇒ On a maintenant tous les outils pour comprendre la diffraction. On va s'intéresser aux figures de quelques objets

II. Illustration sur quelques figure usuelles

1) Diffraction par une fente rectangulaire

On reprend l'expression obtenue au I. 2) (sur slide):

⇒ Maximum prévu dans la direction de l'optique géométrique.

⇒ Dimension la plus grande de la tâche principale dans la dimension la plus petite du diaphragme. Tâche: (2λD/a; 2λD/b) image sur slide

• Parler de la fente infiniment fine: pas de diffraction selon la longueur de la fente:  code python qui trace l'éclairement et permet de visualiser la figure de diffraction

Manip pour retrouver expérimentalement la largeur d'une fente. Utiliser la caméra avec le bon filtre pour éviter la saturatation, mesurer la tache centrale avec ImageJ, remonter à la largeur de fente (cf code Python)

Obtention de la formule du python dans le montage avec une lentille:

2) Diffraction par un diaphragme circulaire en incidence normale

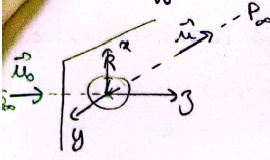
• Symétrie de révolution autour de O_z. Donc I ne dépend que de l'angle (e_z; u) = θ
• On obtient une tâche d'Airy (tâche centrale):

• Rayon angulaire de la tâche d'Airy: sinθ = 0.6 λ/R ≈ θ car λ<<R
• On peut généraliser avec un diaphragme quelconque de dimension caractéristique ρ dans une certaine direction. Alors la tâche de diffraction dans cette même direction a une étendue angulaire: θ≈ λ/ρ

Si ρ augmente, θ diminue

3) Critère de Rayleigh

• Système optique rigoureusement stigmatique (A₁ → A₁'  et A₂ → A₂')
• Mais le faisceau lumineux est limité spatialement pas un ou plusieurs diaphragmes (montures de lentilles, pupilles de l'oeil, ... ), donc il existe de la diffraction, donc on obtient des tâches de diffraction au lieu d'images ponctuelles.  image sur slide
• La diffraction limite le pouvoir séparateur/ le pouvoir de résolution du système optique, c'est à dire la capacité du système optique à donner des images distinctes d'objets proches.
• Critère de Rayleigh: Deux tâches de diffraction peuvent être distinguées si le maximum principal de l'une est au-delà du 1er minimum nul de l'autre.
• Pour séparer A₁ et A₂, il faut A₁'A₂'>R_airy
• ATTENTION: La diffraction n'est pas le seul phénomène à limiter le pouvoir séparateur
  • Défauts des surfaces optiques
  • Effet du capteur
  • Les lunettes astronomiques sont aussi perturbées par la turbulence atmosphérique (variation locales et spatiales de l'indice de l'air)

⇒ La diffraction est une limitation de résolution. Elle peut aussi être exploitée pour modifier des images.

III. Application de la diffraction au filtrage spatial

• Une petite taille caractéristique de l'objet diffractant donne une grande tâche de diffraction.
• Un objet de hautes fréquences spatiales donne une figure de diffraction de basse fréquence spatiale dans le plan de Fourier.

Voir le PDF pour le lien entre transformée de Fourier et filtrage spatial

Monter l'expérience d'Abbe avec comme objet diffractant une grille ou une image rayée et filtrer les hautes fréquences avec une fente

Montage 4f:

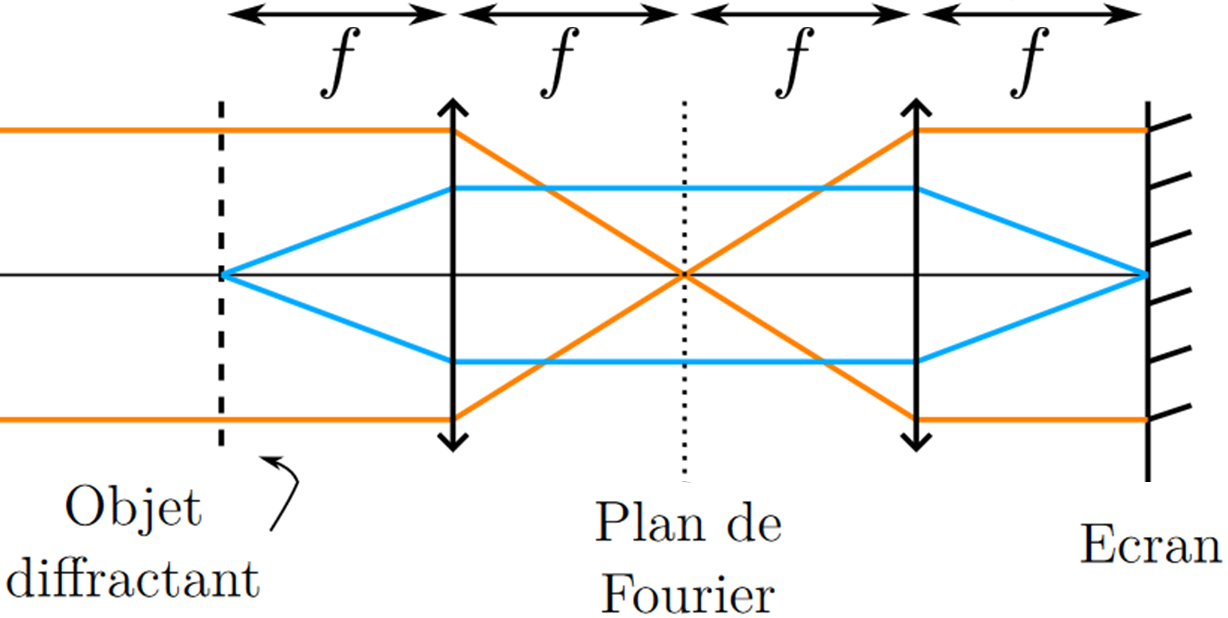
Conclusion

• Application de la diffraction au filtrage d'images et à la strioscopie (visualisation d'objets d'indice de réfraction ou de phase différente).
• Faire attention au critère de Rayleigh.

Code

Tache centrale prise en photo directement sur le capteur de l'appareil photo (visualisée avec l'ordinateur) et mesurée avec imageJ

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import numpy.random as npr

 

In [7]:

# Intensité lumineuse
I0 = 1
lambd = 635e-9  # en nm
a = 200e-6  # largeur de fente
alpha = np.linspace(-0.01, 0.01, 10000)

# Calcul
I = I0 * (np.sinc(np.pi * a * alpha / lambd / np.pi))**2

# Représentation graphique
plt.figure()
plt.plot(alpha, I)
plt.xlim([- 3 * lambd / a, 3 * lambd / a])
xticks_positions = [-3 * lambd / a, -2 * lambd / a, -lambd / a, 0, lambd / a, 2 * lambd / a, 3 * lambd / a]
xticks_labels = [r'$ \frac{-3 \lambda}{a}$', r'$ \frac{-2 \lambda}{a}$', r'$ \frac{- \lambda}{a}$', '0', r'$ \frac{\lambda}{a}$', r'$ \frac{2 \lambda}{a}$', r'$ \frac{3 \lambda}{a}$']
plt.xticks(xticks_positions, xticks_labels)
plt.xlabel(r'$\alpha$',color='green')
plt.ylabel('I', color='green')
plt.title('Diffraction par une fente fine', color='green')
plt.grid()
plt.show()

 

 

# Données
lambd =  # en nm - longueur d'onde du laser

dX =  # en mm - taille de la tache centrale - mesurée avec imageJ
udX = 0.05e-3  # en mm

D =  # en m - focale de la lentille pour faire une image nette sur l'écran
uD = 2e-3  # en m

# Calcul de la largeur de la fente a
a = 2 * lambd * D / dX
ua = a * np.sqrt((udX/dX)**2 + (uD/D)**2)

print('La valeur de largeur de fente expérimentale est: a = ', np.round(a*10**6, 2), ' +- ', np.round(ua*10**6, 2), 'µm')
print('La valeur de largeur de fente théorique est: a = 200µm')

La valeur de largeur de fente expérimentale est: a =  190.5  +-  4.93 µm
La valeur de largeur de fente théorique est: a = 200µm