Créer un site internet
  1. Accueil
  2. Leçons physique
  3. 2024
  4. 10. Induction électromagnétique.

10. Induction électromagnétique.

PPT

Induction electromagnetiqueInduction electromagnetique (13.3 Mo)

 

InductionInduction (2.17 Mo) : leçon présentée dans l'année format 1h

 

L2

Prérequis

  • Electrostatique et magnétostatique (équations de Maxwell, énergie électromagnétique, ARQS, forces de Laplace et de Lorenz)
  • Electrocinétique courant continu (loi d'Ohm locale)
  • Mécanique du point

Introduction

  • On va commencer par une manipulation qualitative: l'expérience de Faraday:
    • Bobine branchée à une faible résistance, on observe la tension aux bornes de la résistance avec un oscilloscope.
    • On bouge un aimant rapidement à proximité d'une bobine fixe ou on bouge une bobine à proximité d'un aimant fixe.
    • On observe E =/= 0 à l'oscilloscope.
  • Interprétation: la condition pour voir un phénomène d'induction dans un circuit est que le champ magnétique traversant le circuit varie dans le temps.

I. Description du phénomène d'induction

1) Flux du champ magnétique à travers une surface

  • Spire plane:

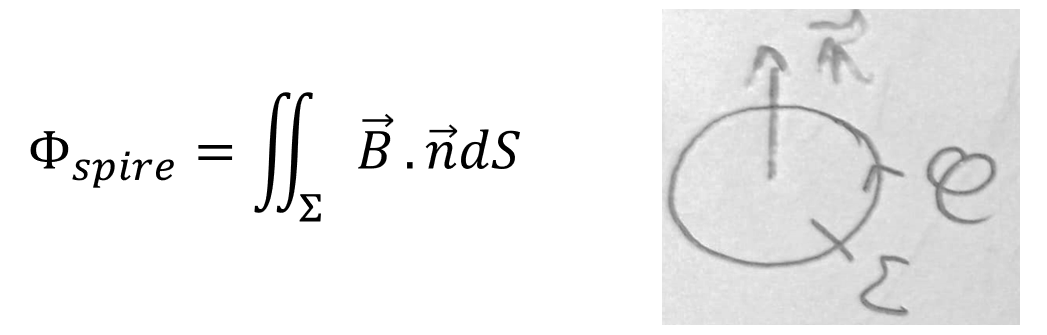
Flux spire

  • Bobine:

Flux bobine

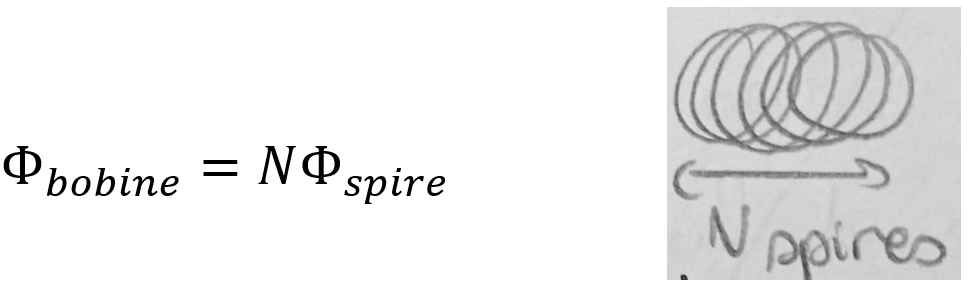
2) Force électromotrice induite

  • Le courant induit dans un circuit fermé est lié à l'apparition d'une force électromotrice induite, qui joue le même rôle que celle d'in générateur.
  • Schéma équivalent (en convention générateur):

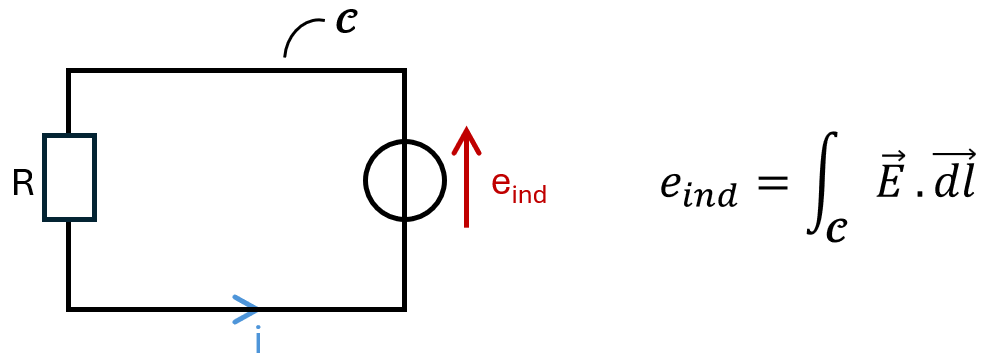
Fem induite

3) Interprétation de l'expérience de Faraday

On va étudier deux cas extrème d'induction dans la suite de ce cours:

  • Circuit indéformable et fixe, B(t) champs magnétique variable dans le temps

    e =/= 0  INDUCTION DE NEUMANN

  • Circuit déformable et mobile, B indépendant de t champ magnétique stationnaire

    e =/= 0 INDUCTION DE LORENTZ

II. Induction de Neumann

1) Loi de Faraday

Loi faraday 1

2) Inductance propre et inductance mutuelle

  • Lorsque le courant dans une bobine est variable, la flux du champ magnétique créé par la bobine, flux propre, est variable.
  • Ceci induit une fem dans la bobine (fem d'auto-induction), qui s'oppose à la variation du courant qui lui donne naissance.

→ Retard à l'allumage quand il y a des bobines dans le circuit

  • Inductance propre L (en Henry, toujours > 0):

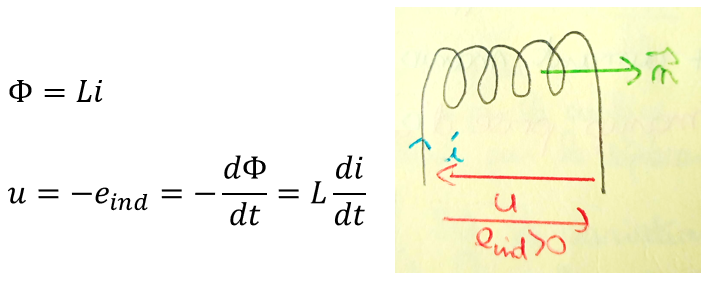
Inductance propre

  • Inductance mutuelle M: Lorsque deux circuits sont en présence, le flux magnétique à travers l'un d'entre eux comporte son flux propre, mais aussi le flux du champ magnétique généré par l'autre circuit.

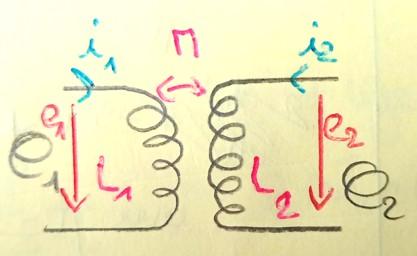
Inductance mutuelle

Flux à travers C2 du champ généré par C1: Phi12

Flux à travers C1 du champ généré par C2: Phi21

3) Energie magnétique

Energie magnetique

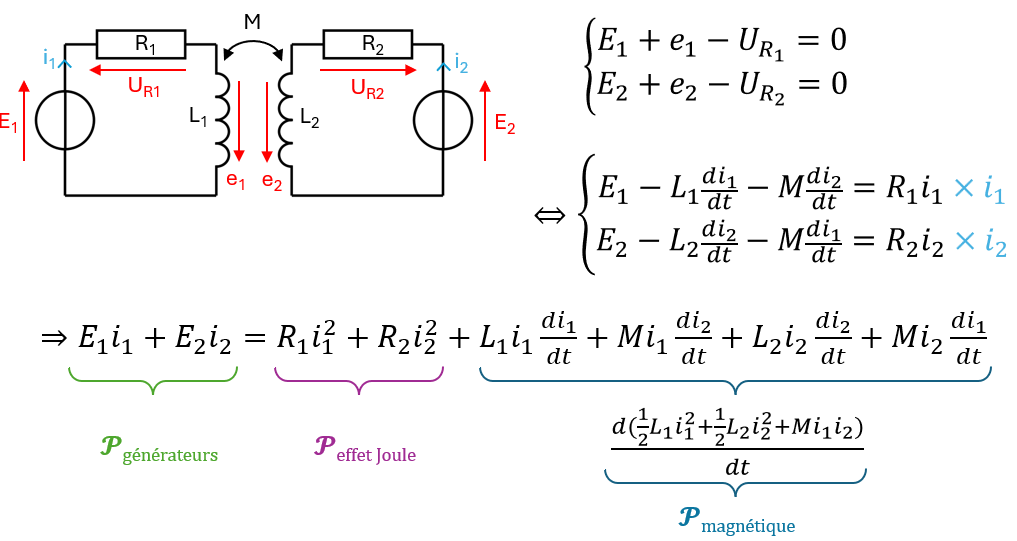
  • Em: Energie magnétique qu'on dû fournir les générateurs aux deux circuits pour créer le champ magnétique.

4) Induction de Neumann dans les circuits non-filiformes: application au freinage inductif

  • Lorsque le conducteur est un bloc de métal plongé dans un champ magnétique temporellement variable, l'induction de Neumann se manifeste par des courants volumiques appelés courants de Foucault.
  • Manip dans le tube en PVC et le tube en cuivre.
  • Quali dans les deux tubes puis prise d'un point en direct.
  • Avec les points en préparation + le point en direct on trace z(t) et on compare les courbes.
  • On en déduit qu'on peut modéliser les courants de Foucault comme des frottements fluides dans le tube en cuivre.
  • On fait ensuite l'analyse théorique:

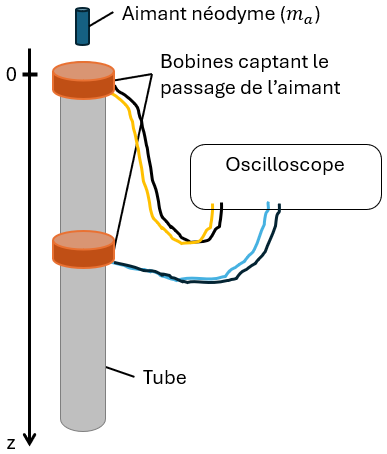
Tubes

  • Tube en PVC:

BdF: P = mag

PFD: maa = mag

Donc en chute libre: z(t) = gt2/2

  • Tube en cuivre:

BdF: P = magv
         Ff = - αv   → modélisation par des frottements fluides

PFD: ma dv/dt = mag - αv 
        v - τ dv/dt = vlim
avec: τ = ma / α à calculer    et:   vlim = ma g / α   à calculer
⇒v(t) = vlim(1 - e -t/τ)  et   z(t) = vlim t + vlim τ (e -t/τ - 1)
Calculer llim

III. Induction de Lorentz - Circuit mobile dans B fixe

1) Changement de référentiel

  • On considère une charge ponctuelle q en mouvement dans un laboratoire.
  • R: référentiel du laboratoire supposé galiléen (E, B)
  • R': référentiel galiléen en translation par rapport à R à la vitesse vR'/R = ve (E', B')
  • Si ve << c: E' = E + ve ^ B   dans l'ARQS magnétique d'après l'égalité des forces de Lorentz dans les différents référentiels

                     B' = B

Démonstation

Utile surtout à partir de l'équation 14.6:

  • Egalité des deux forces de Lorentz
  • Formule de changement de référentiel
  • Egalité de tout ça

Demo changement ref

2) FEM de Lorentz

Par définition, on a:

Fem lorentz

⇒ La loi de Faraday est généralisable avec §Ø (delta flux) la variation du flux du champ magnétique à travers le circuit lors du déplacement du circuit pendant §t.

3) Rails de Laplace

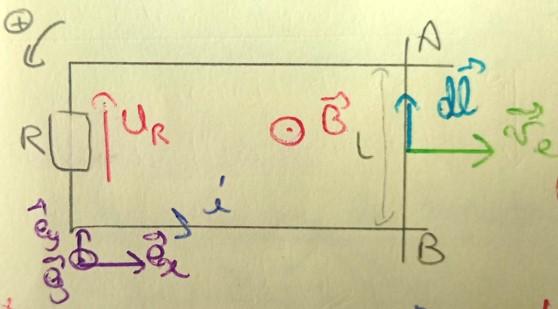
Rail laplace

  • Rails + tige = conducteurs parfaits

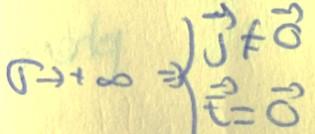
Conducteurs parfaits

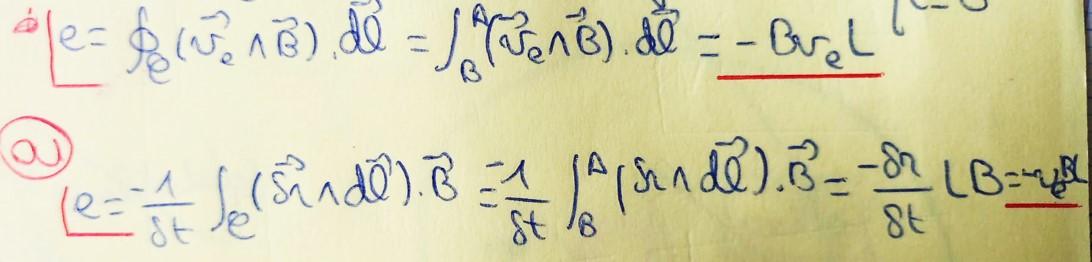
  • Fem rail laplace
  • e = - UR = - R i     ⇒    i = ve B L / R > 0
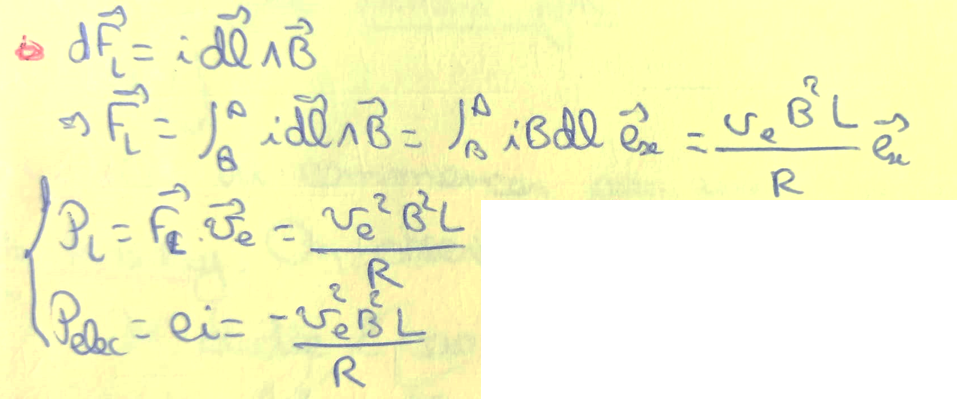
  • Puissance laplace

⇒ PLaplace = - Pélec    ⇒ Conversion de puissance électrique en puissance mécanique

Conclusion

En conclusion l'induction électromagnétique est un phénomène qui a de nombreuses applications dans la vie quotidienne:

  • Courants de Foucault exploités pour les plaques à induction et le freinage
  • Courants de Foucault non voulus dans les transformateurs, donc ils sont "feuilletés"
  • Conversion électromécanique avec le haut parleur ou la machine à courant continu

Bonus

Code

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import numpy.random as npr

# Definition de la fonction affine
def f_aff(x, a, b):
    return a * x + b

# Montecarlo
def montecarlo(X, Y, uX, uY, N_mc=100):
    sigma_X = uX*np.ones(X.size)
    sigma_Y = uY*np.ones(Y.size)

    param = np.zeros((2,N_mc))
    for i in range(N_mc):
        x_mc = npr.normal(loc=X, scale=sigma_X)
        y_mc = npr.normal(loc=Y, scale=sigma_Y)
        pop, pcov = curve_fit(f_aff, x_mc, y_mc)
        param[0,i] = pop[0]
        param[1,i] = pop[1]

    x_th = np.linspace(X.min(), X.max(), 4)
    y_th = f_aff(x_th, *pop)
    for i in range(N_mc):
        y_th = f_aff(x_th, *param[:,i])
        plt.plot(x_th, y_th, 'r', alpha=0.05)
    plt.errorbar(X, Y, xerr=uX, yerr=uY, fmt='+', capsize=3, label='expérimentale')
    # plt.show()

    a_moy = np.mean(param[0,:])
    a_sig = np.std(param[0,:]) #ecart type
    b_moy = np.mean(param[1,:])
    b_sig = np.std(param[1,:]) #ecart type
    print("La pente moyenne sur les ", N_mc, "mesures est de :", np.round(a_moy,4))
    print("L'écart type entre les pentes des", N_mc, "mesures est de :", np.round(a_sig,4))
    print("Le résultat est donc de :", f"a = {a_moy:.3f} +/- {a_sig:.3f}")
    print("Cela correspond à une erreur de:", f"a_rel = {a_sig/a_moy*100:.0f} %")
    return (a_moy, a_sig, b_moy, b_sig)

# Definition de la fonction plynomiale d'ordre 2
def f_poly_2(x, a, b, c):
    return a * x**2 + b * x + c

# Montecarlo
def montecarlo_poly_2(X, Y, uX, uY, N_mc=100):
    sigma_X = uX*np.ones(X.size)
    sigma_Y = uY*np.ones(Y.size)

    param = np.zeros((3,N_mc))
    for i in range(N_mc):
        x_mc = npr.normal(loc=X, scale=sigma_X)
        y_mc = npr.normal(loc=Y, scale=sigma_Y)
        pop, pcov = curve_fit(f_poly_2, x_mc, y_mc)
        param[0,i] = pop[0]
        param[1,i] = pop[1]
        param[2,i] = pop[2]

    x_th = np.linspace(X.min(), X.max(), 100)
    y_th = f_poly_2(x_th, *pop)
    for i in range(N_mc):
        y_th = f_poly_2(x_th, *param[:,i])
        plt.plot(x_th, y_th, 'r', alpha=0.05)
    plt.errorbar(X, Y, xerr=uX, yerr=uY, fmt='+', capsize=3, label='expérimentale')
    # plt.show()

    a_moy = np.mean(param[0,:])
    a_sig = np.std(param[0,:]) #ecart type
    b_moy = np.mean(param[1,:])
    b_sig = np.std(param[1,:]) #ecart type
    c_moy = np.mean(param[2,:])
    c_sig = np.std(param[2,:]) #ecart type
    print("La pente moyenne sur les ", N_mc, "mesures est de :", np.round(a_moy,4))
    print("L'écart type entre les pentes des", N_mc, "mesures est de :", np.round(a_sig,4))
    print("Le résultat est donc de :", f"a = {a_moy:.3f} +/- {a_sig:.3f}")
    print("Cela correspond à une erreur de:", f"a_rel = {a_sig/a_moy*100:.0f} %")
    return (a_moy, a_sig, b_moy, b_sig, c_moy, c_sig)

## <font color="purple">Trajectoire de l'aimant dans un tube</font>

### <font color="blue">Trajectoire de l'aimant dans un tube en PVC</font>

><div class="alert alert-block alert-warning"> $$ z(t) = \frac{gt^2}{2} $$
 

# Mesures de préparatation
z = np.array([])  # en m. Position du haut de la bobine basse par rapport au haut de la bobine haute
uz = 2e-3  # en m  
t = np.array([])  # en s. Temps de trajet de l'aimant d'une bobine à la suivante
ut = 4e-3  # en s

# Mesures de présentation
z_mesure = np.array([])  # en m
t_mesure = np.array([])  # en s

# Montecarlo
a_moy, a_sig, b_moy, b_sig, c_moy, c_sig = montecarlo_poly_2(np.concatenate([t, t_mesure]), np.concatenate([z, z_mesure]), ut, uz, N_mc=100)
plt.xlabel("Temps (s)")
plt.ylabel("Position (en m)")
plt.title("Evolution de la position de l'aimant en fonction du temps")
plt.plot(t_mesure, z_mesure, 'o', color='green')
plt.errorbar(t_mesure, z_mesure, xerr=ut, yerr=uz, fmt='+', capsize=3, color='green')

# Données
g = 9.81  # en m.s-2
ma =  # en kg petit aimant
uma = 0.1e-3  # en kg

# Graphe théorique
z_th = g * t**2 / 2
plt.plot(t, z_th, color='purple', label='theorique')
plt.legend()
plt.show()

### <font color="blue">Trajectoire de l'aimant dans un tube en cuivre</font>

><div class="alert alert-block alert-warning"> $$ z(t) = v_{lim}t + v_{lim}\tau (e^{-\frac{t}{\tau}} - 1) $$

# Mesures de préparatation
z = np.array([])  # en m. Position du haut de la bobine basse par rapport au haut de la bobine haute
uz = 3e-3  # en m  

t = np.array([])  # en s. Temps de trajet de l'aimant d'une bobine à la suivante
ut = np.array([])  # en s

# Mesures de présentation
z_mesure = np.array([])  # en m
t_mesure = np.array([])  # en s

# Montecarlo
a_moy_cu, a_sig_cu, b_moy_cu, b_sig_cu = montecarlo(np.concatenate([t, t_mesure]), np.concatenate([z, z_mesure]), ut, uz, N_mc=100)
plt.plot(t_mesure, z_mesure, 'o', color='green')
plt.errorbar(t_mesure, z_mesure, xerr=ut[-1], yerr=uz, fmt='+', capsize=3, color='green')
plt.xlabel("Temps (s)")
plt.ylabel("Position (en m)")
plt.title("Evolution de la position expérimentale\nde l'aimant en fonction du temps")

# Données
g = 9.81  # en m.s-2
ma =  # en kg petit aimant
uma = 0.1e-3  # en kg

# Vitesse limite
print('')
print('La vitesse limite de l\'aimant vaut vlim = ', np.round(a_moy_cu, 2), '+-', np.round(a_sig_cu, 2), 'm/s')

alpha = g * ma / a_moy_cu
ualpha = alpha * np.sqrt((uma/ma)**2 + (a_sig_cu/a_moy_cu)**2)
print('Le coefficient de frottement vaut alpha = ', np.round(alpha, 2), '+-', np.round(ualpha, 2), 'kg.s-2')

tau = ma / alpha
utau = tau * np.sqrt((uma/ma)**2 + (ualpha/alpha)**2)
print('Le temps caractéristique vaut tau = ', np.round(tau * 10**3, 1), '+-', np.round(utau * 10**3, 1), 'ms')

llim = a_moy_cu * 5 * tau + a_moy_cu * tau * (np.exp(- 5 * tau / tau) - 1)
ullim = llim * np.sqrt((a_sig_cu/a_moy_cu)**2 + (utau/tau)**2)
print('La longueur du régime transitoire vaut llim = ', np.round(llim * 10**3, 1), '+-', np.round(ullim * 10**3, 1), 'mm')


# Graphe théorique
t_th = np.linspace(0, t[-1], 100)
x_th = a_moy_cu * t_th + a_moy_cu * tau * (np.exp(-t_th / tau) - 1)
plt.plot(t_th, x_th, color='purple', label='theorique')
plt.legend()
plt.show()

### <font color="blue">Trajectoire de l'aimant dans un tube en aluminium</font>

# Mesures de préparatation
z = np.array([])  # en m. Position du bas de la bobine basse par rapport au bas de la bobine haute
uz = 3e-3  # en m  

t = np.array([])  # en s. Temps de trajet de l'aimant d'une bobine à la suivante
ut = 10e-3  # en s

# Mesures de présentation
z_mesure = np.array([])  # en m
t_mesure = np.array([])  # en s

# Montecarlo
a_moy_alu, a_sig_alu, b_moy_alu, b_sig_alu = montecarlo(np.concatenate([t, t_mesure]), np.concatenate([z, z_mesure]), ut, uz, N_mc=100)
plt.xlabel("Temps (s)")
plt.ylabel("Position (en m)")
plt.title("Evolution de la position de l'aimant en fonction du temps")
plt.plot(t_mesure, z_mesure, 'o', color='green')
plt.errorbar(t_mesure, z_mesure, xerr=ut, yerr=uz, fmt='+', capsize=3, color='green')

# Données
g = 9.81  # en m.s-2
ma =  # en kg petit aimant
uma = 0.1e-3  # en kg

# Vitesse limite
print('La vitesse limite de l\'aimant vaut vlim = ', np.round(a_moy_alu, 2), '+-', np.round(a_sig_alu, 2), 'm/s')
alpha = g * ma / a_moy_alu
ualpha = alpha * np.sqrt((uma/ma)**2 + (a_sig_cu/a_moy_cu)**2)
print('Le coefficient de frottement vaut alpha = ', np.round(alpha, 2), '+-', np.round(ualpha, 2), 'kg.s-2')

# Graphe théorique
t_th = np.linspace(0, t[-1], 100)
x_th = a_moy_alu * t_th + a_moy_alu * ma / alpha * (np.exp(-t_th * alpha / ma) - 1)
plt.plot(t_th, x_th, color='purple', label='theorique')
plt.legend()
plt.show()

Date de dernière mise à jour : 13/06/2024